量子随机性与量子随机数发生器的发展

|作者：刘宇轩　白玉明　李俊林†

(清华大学物理系 低维量子物理全国重点实验室)

本文选自《物理》2025年第10期

摘 要：随机数是信息安全的基石。信息加密的安全性来源于随机数的不可预测性，高随机性的随机数发生器是密码学的重要需求。随机性作为随机数最重要的性质一直被广泛讨论与研究。文章介绍了随机性的基本特性、随机数发生器的发展历程、量子随机数发生器的量子优势及近年国内外在该领域的发展状况。

关键词：量子随机数发生器，内禀随机性，量子性

01引 言

信息安全是社会稳定的必要条件，信息网络空间已经成为继陆、海、空、天外的第五维国家安全领域。信息安全技术涵盖了许多学科，其中密码学是最重要的部分之一。传统密码技术包含了对称密码、公钥密码、数字签名等，直至今日，它们在信息安全中依然发挥着重要作用。信息安全事件例如网络攻击、数据泄露、基础设施入侵等往往会对国家安全、经济稳定甚至国际关系造成严重影响。

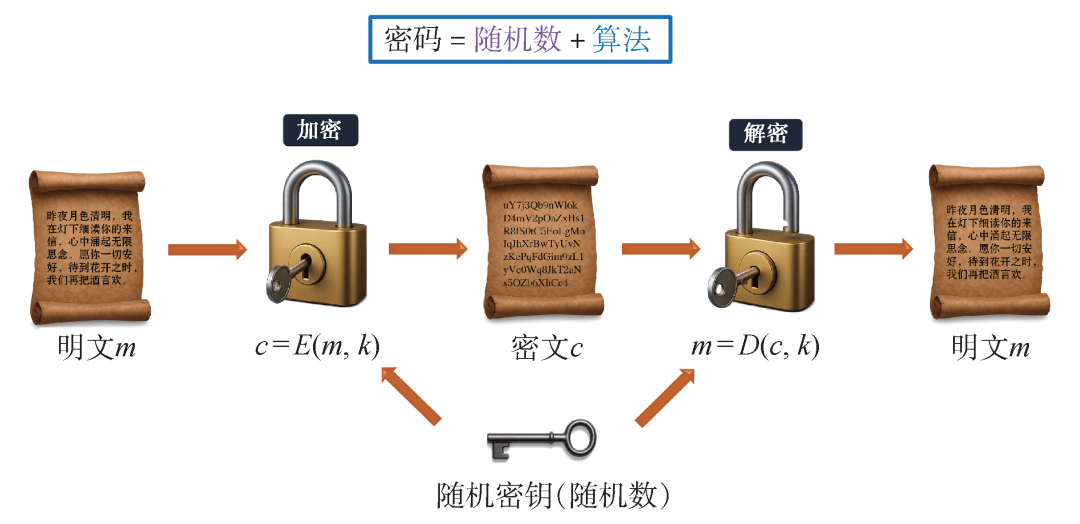图1　经典密码系统的原理

密码由随机数和算法组成。如图1所示，经典密码技术基于算法(例如加密函数E(m, k)与解密函数D(c, k)，其中k为密码算法的密钥，是加解密函数的一个参量，通常是一段特定长度的随机数)实现明文(简写为m)与密文(简写为c)的相互转换，其侧重点在于算法，即通过采用复杂的算法，让破解密钥的时间远长于密码保护信息的有效期。通俗来说，就是采用一道困难的数学题来保护信息，在现有计算机的计算能力下，需要很多年(大于50年)才能破解。与之相反的，对于随机数的态度是够用就行。因此当前许多密码系统大多采用基于数学算法的伪随机数，稍好一点的是采用基于经典物理过程的随机数(如电噪声、热噪声等)。

需要说明的是，加密算法一般是公开的，即题目是公开的。即使是不公开的加密算法也存在着被破解的可能性：1999年，DVD的密码算法被破解；2007年，NXP公司的非接触IC卡产品(MIFARE Classic)的密码算法被破解；大名鼎鼎的RSA公司开发的RC4算法也被破解。

随机数和算法共同构成了密码，因此密码的安全性也就依赖于随机数的安全性与算法的安全性。经典的加密技术安全性侧重于算法的安全性，但算法的安全性是有条件的，即要求攻击者的计算能力在某一限定值下才能够保证安全，而量子计算机的强大算力颠覆了算法安全性的条件。并且量子计算机的能力极限目前仍无定论，因此在算法无法保证安全性的情况下，必须依赖随机数的质量来保证安全性。简单来说就是对整个密码系统，应当保证即使算法被破译，信息仍然是安全的。

量子计算机的出现使得计算能力出现指数级的巨大提升。2024年谷歌最新的量子计算芯片Willow在5分钟内完成了一项随机电路的采样计算，而目前顶尖超算完成该计算需要超10^25年(超过宇宙年龄)。今年国内成功构建的超导量子计算原型机“祖冲之三号”也比目前最快的超算快千万亿倍，再次打破超导体系量子计算优越性世界纪录。依赖于数学算法的密码安全性在量子计算机强大的算力下非常脆弱，很容易被量子计算机破解。例如著名的RSA公钥系统基于两个较大质数p、q与它们的乘积N=pq 生成密钥，其安全性依赖于大数分解问题，即找到N的两个因子p、q 的困难性。而早在1994年，Shor就提出了能够有效解决大数分解问题的量子算法，证明量子计算机能够轻易破解RSA公钥系统。

一旦足够强大的量子计算机投入使用，许多互联网通信、数字签名、密码、合同和其他文件的数据保护机制将立即过时。此外，攻击方可能会现在就下载并存储密文数据，然后在量子计算机足够强大时再进行解密。这种策略被称为“现在收集，未来解密”，在未来可能会造成敏感信息泄露，危及国家安全。因此，密码体系的安全性提升刻不容缓。

在量子计算机时代，加密技术的安全性将更侧重于随机数的安全性。例如量子密钥分发(quantum key distribution，QKD)，作为量子威胁的应对方案之一，随机数替代了算法成为安全性的主要部分。当量子密钥分发协议中随机选择的测量基能够被攻击者有效预测时，协议将不再具有安全性[1，2]。而随机数的安全性来源于随机数的随机性，高随机性的随机数是密码系统的基石。量子随机数发生器即将成为密码系统的重要基础设施，我国工信部也正在加紧制定量子随机数发生器行业规范。下面我们将对随机数的随机性、随机数发生器的发展与量子随机性进行介绍。

02随机数的随机性

随机性是随机数的本质属性。冯·米塞斯、马丁-洛夫、柯尔莫戈洛夫等著名数学家都对随机性的科学定义进行了长时间的研究与讨论[3，4]。最终，马丁-洛夫基于柯尔莫戈洛夫复杂性(柯氏复杂性)的理论形式化地给出了“随机性”的定义[5，6]：一个二进制序列x是随机的，当且仅当它的柯尔莫戈洛夫复杂度K(x)接近其自身长度|x|，即：

K(x) ≥ |x| - c (c 为常数).

通俗来说就是指不存在比x本身短得多的程序来生成x，即它没有简洁的规律性描述。马丁-洛夫在柯氏复杂性的基础上将随机性定义为能通过所有有效的统计测试，并证明对于无限长序列而言二者的等价性[6]，通俗而言就是通过数据统计的方法无法找到序列存在的任何规律。二者都从不可计算性的角度给出了随机性的描述，成为了现代密码学、随机性检测理论的严格数学基础。在这一定义下，已经制定一些证明不可计算随机性的标准，例如美国国家标准技术研究所(NIST)的NIST SP 800-22规范[7]与中国国家密码管理局的GM/T0005-2021随机性检测规范[8]。

需要注意的是，虽然以上定义的随机性具有严格的数学形式，但它并不是本文所说的真随机性。柯尔莫戈洛夫本人也清楚这一点：“通常理解的随机过程是指无法找到规律、无法预测结果的过程。在概率论的应用中，我们需要区分随机性(没有任何规律性)和统计随机性(概率论的主题)。概率论无法否定随机过程中可能存在的规律性，它仅仅是从实际现象的统计随机性假设中推导出一些正确的结论[9，10]”。

综上，柯氏复杂性定义的随机性仅证明了序列具有不可计算的特性，即这个序列看起来足够“混乱”，但这并不意味着序列是不可预测的，因此它并不是真随机性的定义。真随机性的定义一直处于讨论之中，但从目前的结果来看，许多数学家对从数学上给出随机性的严格定义持悲观态度。汉斯-弗赖登塔尔说道：“任何试图以规范的方式来定义无序的尝试都会走入矛盾。虽然无序的概念并不矛盾，但当我试图将其规范化时，情况就是如此”[11]。

数学严格定义随机性的困难在于随机性是产生随机序列过程的特性，而不是序列本身的特性。数学定义的本质是划定一个满足随机性条件的序列的标准，然而一个真随机过程可能产生任何序列(所有序列都是等概率出现的)，而同样的序列也能由确定性过程生成(例如计算机程序)，因此一个序列是否随机无法通过制定一个确定的标准来定义，即序列的产生方法影响着这个序列是否随机。举一个通俗的例子，π的十进制序列能够通过统计测试，满足柯氏复杂性定义的随机性，但显然它并不是随机的。正如冯·诺依曼所言：“没有所谓的随机数，只有产生随机数的方法[12]”。

从以上的分析中可以看出，本文所讨论的随机性是随机过程或随机源不可预测的真随机性，而非序列不可计算的统计随机性。虽然真随机性的严格定义尚未有定论，但在漫长的讨论中可以总结出真随机序列应当具备以下特性：

(1)无限长

随机源能够输出无限长的序列，不会在有限长输出后重复之前的输出，输出序列不存在周期性。在密码学应用中，不满足该特性的随机源一旦输出序列超过最大长度后，攻击者能对序列进行完全预测。

(2)不可计算

随机源的输出序列具有良好的柯氏复杂性，能够通过所有有效的统计检测，无法利用序列的前n位有效预测第n+1位的值。满足该特性的随机源在密码学应用中能保证一定条件下的安全，即在攻击者仅能获取其他输出序列的条件下保证序列安全。例如使用圆周率π的十进制序列来进行加密，若攻击者不知道序列来源，则能保证安全。但若攻击者具有随机源信息，例如序列来源于π，则能够对序列进行有效预测。

(3)不可预测

随机源的输出序列无法预测，即使攻击者获取了随机源全部的状态信息与环境信息，也无法预测随机源的输出。满足该特性的随机源在密码学应用中能无条件保证输出序列的安全。

需要注意的是，以上的三个特性是递进的关系：有限长的序列总可以被完整描述，因此必然是可计算的；可计算的序列，将计算视为预测方法的一个特例，其必然是可预测的。从无限长、不可计算到不可预测，随机源的随机性在不断提升，恰好对应了随机数发生器的发展历程。

03随机数发生器发展历程

随机数发生器是用于产生随机数的机器，对信息安全、数学与物理计算(如Monte Carlo算法)、人工智能与机器学习、金融工程与经济学等领域都具有重大意义，其发展历程对应着随机性不断提升的历程，如图2所示。围绕着随机数的无限长、不可计算和不可预测特性，从最早的基于算法的随机数发生器发展到基于物理源的随机数发生器(实现无限长与不可计算)，又发展到了量子随机数发生器(实现不可预测)。

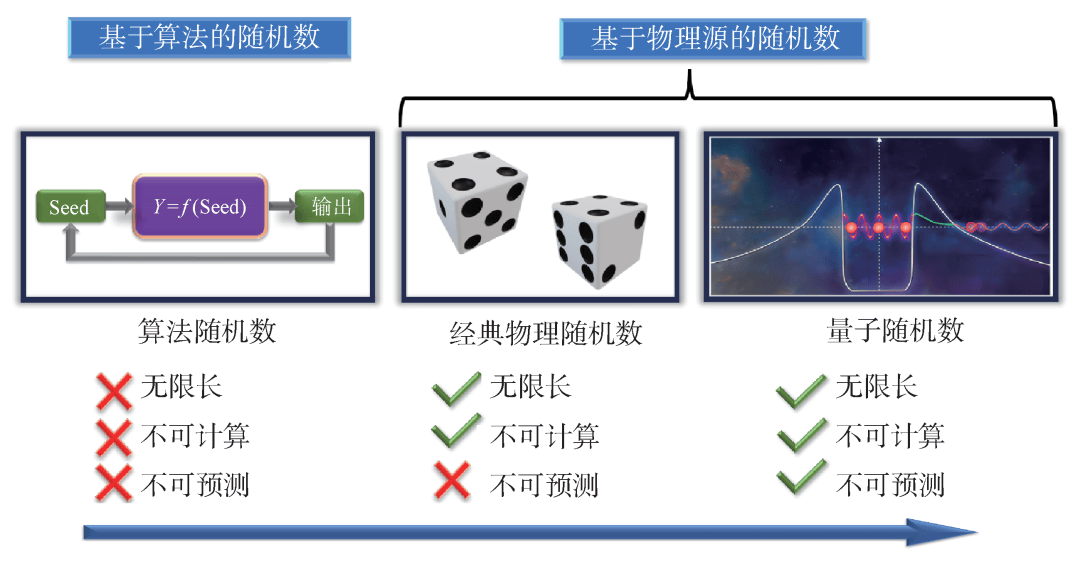图2　随机数发生器发展历程

1946年，伪随机数发生器(pseudo-random number generator，PRNG)被提出[12]，其基本思想是将随机数种子(一串序列)输入算法得到一个输出，再将该输出作为新的种子计算下一个输出，反复迭代输出随机序列。PRNG的出现大大提升了随机数生成率，满足了许多应用的需求。但在实际应用中，由于PRNG种子长度有限，取值空间有限，导致PRNG无论从什么种子开始，最终都会进入有限状态的循环，意味着PRNG的输出是周期性重复的有限长序列。这是PRNG种子空间有限和确定性演化的必然结果，可以将种子序列比喻成手串上的珠子，将PRNG算法比喻成两两连接珠子的链条，由于珠子的数量有限，有限次连接后必然形成环，对应PRNG种子回到之前的状态，开始周期性输出。因此PRNG不具备无限长特性，那么必然也是可计算与可预测的，难以满足密码学对于序列安全的要求。

为了解决PRNG周期性输出问题，人们开始利用实际的物理系统生成随机数。最直接的方法是通过宏观经典物理系统生成随机数，如系统噪声或对初始条件敏感的混沌物理系统[13，14]。实际物理系统具有无穷多可能的状态，不存在有限次演化必然回到初始状态的问题，可输出无限长序列。经典物理随机数发生器利用经典物理系统的随机信号，配合数学后处理过程，输出的序列能够通过大多数统计测试，基本满足了随机性不可计算的特性，一定程度上能够满足信息安全的基本要求。因此，为与PRNG相区分，有人称它们为真随机数发生器(true random number generator，TRNG)。但从物理学的视角来看，经典物理系统是可预测的，所以TRNG产生的序列并不是真随机数。经典物理系统由确定的动力学方程描述，本质上和PRNG仅存在状态空间大小的区别，若获取了系统的状态信息，就能对系统进行预测。即使实际物理系统复杂度高，难以给出准确动力学描述，系统状态也随时间连续演化，带宽有限，信号在局域时间内必然存在关联，攻击者只要获取足够的信息，就能对系统的状态演化进行预测。与PRNG相比，经典物理随机数具备无限长与不可计算特性，能够一定程度满足信息安全的需求，但其原理上仍是确定性的，不具备不可预测性。

而量子随机数发生器(quantum random number generator，QRNG)在原理上满足了不可预测性。在量子力学的哥本哈根诠释中[15]，量子态测量坍缩结果具有内禀随机性，即使获得了量子态所有的信息，也无法预测坍缩结果；坍缩时间是瞬时的，等效带宽无穷大，前后坍缩结果不存在任何关联性。因此QRNG自2000年开始逐渐受到广泛关注[16]。与经典随机数发生器相比，QRNG在具备无限长、不可计算特性的基础上，根据量子力学的波函数测量坍缩假设，原理上保证了输出序列的不可预测性，这就是QRNG相比于经典随机数发生器的量子性优势。下一节会详细分析经典系统和量子系统在随机性上的区别。

04两种随机性：表观随机性与内禀随机性

经典系统与量子系统均能够实现随机序列输出，但两者在可预测性上存在着本质区别，由此引出了两类随机性的概念：表观随机性与内禀随机性。

表观随机性是对于系统状态与演化缺乏足够的信息而展现的随机性。若得到系统状态与演化的信息，则系统演化是可预测的。经典系统的随机性为表观随机性，例如大气系统、电磁噪声等。表观随机性对经典力学研究有重要意义，与统计力学的基本假设具有深刻联系[17]，很多复杂系统内部遵循确定性的演化规律，但基于概率论的假设引入随机数进行分析也能得到有意义的结论。即使经典系统的某些特性和概率论中随机过程的特性吻合，也不意味着系统的随机性是真实的，正如冯·诺依曼所言[12]：“一些用随机方法解决的问题可能存在使用更严格序列解决的可能”。理论上，所有经典物理系统展现的随机特性均属于表观随机性，信息客观存在，系统并非不可预测。如图3所示，著名的比喻拉普拉斯妖指出了经典物理系统表观随机性可预测的本质[18]：“有一个智者，在给定的时刻，了解了自然界中的所有物质的能量与动量，它足够强大，可以对这些数据进行分析，它能以同样的公式描绘宇宙中最大物体和最轻原子的运动。那么对它来说，没有什么是不确定的，未来就像过去一样，在它的眼中同时存在”。在表观随机性的世界(经典物理世界)，所有事件只有一种发展方式，一切看似随机的过程都是可预测的。在密码学应用的角度，利用表观随机性进行加密的本质就是利用一段信息去保护另一段信息，风险始终存在，如果攻击者能够更好地预测随机源，安全性就会被破坏。

图3　拉普拉斯妖对宇宙中一切物质的演化进行预测

内禀随机性指随机性是作为系统内禀属性而存在的，即使了解系统所有的状态信息，也无法预测系统的输出。只有利用具有内禀随机性的随机源才可能实现无条件安全的信息加密。量子力学理论中的叠加态测量随机坍缩正是内禀随机的，它的随机性是系统的内在属性，即使完全了解系统状态，也无法预测叠加态的坍缩结果。

从系统演化的角度看，在经典力学中，只要确定系统某一时刻的坐标与动量，系统状态就被完全确定，之后系统的一切都是完全确定的，不存在随机性，只要提高我们的测量精度与计算设备，就能够以想要的精度对系统演化进行预测。而在量子力学的观点中，量子态存在着内禀随机性，仅能利用概率波函数对系统的演化进行描述，量子力学本质上是概率的。

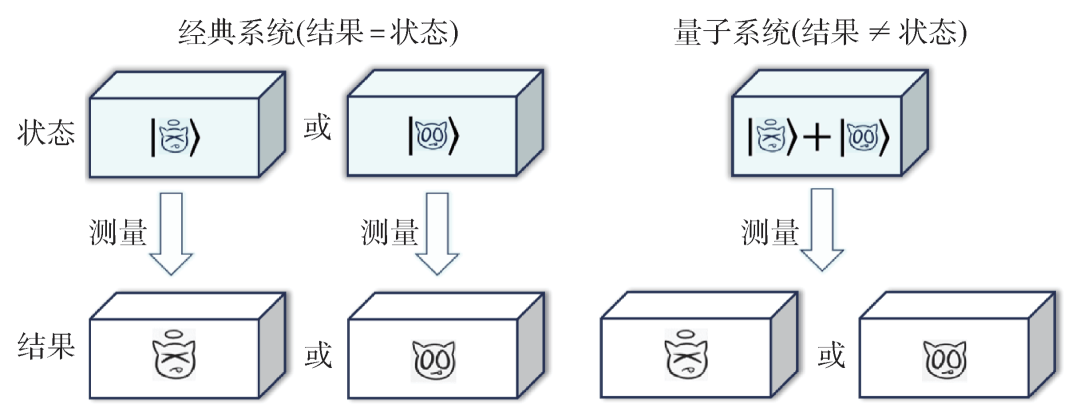图4　经典系统和量子系统的状态与测量结果的关系

从测量的角度看，经典系统的测量结果就是系统所处的状态，测量不影响经典系统的状态，测量结果也随状态而客观存在，即经典系统力学量满足实在论，仅存在表观随机性。而量子系统的测量结果伴随着量子态坍缩，在测量之前该结果并不实际存在。如图4所示，经典系统的测量结果=状态，量子系统的测量结果≠状态。量子系统的结果仅能通过测量坍缩获取，并且在测量后系统坍缩至力学量本征态，系统失去了测量前的状态信息，因此量子系统力学量不满足实在论，具有内禀随机性。定域实在论的讨论也是量子力学基本问题研究的重要部分，持续了近一个世纪，最终通过贝尔不等式的提出与实验验证证明了量子力学不满足定域实在论[19—23]，2022年诺贝尔物理学奖也颁给了在贝尔不等式验证实验中做出贡献的三位学者：阿斯佩(A. Aspect)、克劳泽(J. F. Clauser)与塞林格(A. Zeilinger)。

图5　扔硬币的经典随机过程

以扔硬币为例，这是一个经典随机的典型例子，如图5所示。数学中通常认为硬币的正反面是完全随机的，但实际过程中如果有一个高速相机，对扔出的硬币不停地拍照(观测)，获取硬币足够多的运动信息后是可以预知最终结果的，或者在硬币接近停止时也可以知道结果。

若考虑该问题的量子版本，“量子硬币”从扔出到静止的演化时间是0，中间无法插入任何过程获取信息(例如拍摄)，该随机性由叠加态的内禀随机性保证。

从以上例子可以看出，表观随机性在具有更多信息的攻击者角度可预测，不具备安全性，而内禀随机性保证了无论攻击者获取了多少信息，序列均具有不可预测性。因此只有QRNG能够保证加密系统的安全性，这也是QRNG相比于经典随机数发生器的量子优势。内禀随机性同时保证了随机序列的不可重现性，即使两个完全相同的QRNG在完全相同的条件下工作，其输出结果也是不一样的，二者输出不存在任何的关联性和逻辑性，各自具有独立的随机性，即QRNG产生的随机数具有唯一性。而在经典物理中，在完全相同的条件下抛出两个相同的硬币，两个硬币的结果一定是相同的。不可重现性也是QRNG相比于经典随机数发生器的显著特征。

为何微观粒子具有内禀随机性而大量微观粒子组成的经典系统是确定性的？2024年数学界的诺贝尔奖——阿贝尔奖的获得者米歇尔·塔拉格朗(Michel Talagrand)的结论解释了这一问题[24]：“一个随机变量如果依赖于(以一种“平滑”的方式)许多独立的随机变量(权重不集中在某一个变量上)，那么这个随机变量本质上是一个常量”。即如果一个过程依赖于许多相互独立的随机过程，不同的随机因素不会提高该过程的随机性，反而更加倾向于相互抵消，使得该过程趋向于确定性的过程。经典理论描绘的宏观物体，大量微观粒子的随机性相互抵消，导致宏观物体展现出确定性的运动规律。可以将宏观物体的物理量理解为大量粒子物理量的平均值，量子力学中的埃伦费斯特定理也验证了经典物理与量子物理的联系[25]。在经典极限下，量子期望值的运动方程为

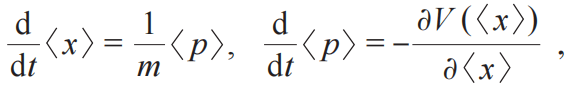
与经典正则方程相对应。可以理解为经典物理是量子物理的“平均效应”，即经典理论包含在了量子理论之中。

在实际应用中，选择量子系统的根本原因是量子系统能够带来超越经典物理框架的优势，因此量子系统的量子性(见Box1)是应用中的一个重要指标。

量子性

当我们称一个系统具有量子性时，并不是因为这个系统使用了量子理论进行描述，而是因为这个系统展现出了无法使用经典理论所解释的特性。以光为例，尽管光的双缝干涉可以用量子理论中的概率波函数干涉进行解释，但也能够使用经典的电磁波理论进行描述，因此光的双缝干涉并没有明显的量子性；而纠缠光子的贝尔不等式违背现象与经典理论的定域实在论存在本质矛盾，经典理论无法解释，即超出了经典理论框架之外，因此光子纠缠就具有显著的量子性。以电子为例，当电子在电场中自由运动时，既可以使用薛定谔方程对波函数波包的运动进行描述，也可以使用经典运动方程对电子运动进行描述，因此自由运动的电子不存在显著的量子性；而当电子被束缚在势阱中时，能够以隧穿方式穿过高于自身能量的势垒从势阱中逃逸，这样的现象无法使用经典理论进行描述，因此电子隧穿具有显著的量子性。同样地，在QRNG领域，并不是QRNG系统能够使用量子理论进行描述，系统就具有了显著的量子性。在QRNG中，只有波函数坍缩的内禀随机性是经典理论无法描述的，由此可以定义出量子随机性与QRNG系统的量子性等概念，下面将对量子随机性与量子性进行详细地分析。

05量子随机性、量子性的定义与特性

基于对量子系统随机性的分析，可以将基于量子叠加态坍缩的内禀随机性定义为量子随机性。

5.1　量子随机性定义

量子随机性是量子叠加态波函数测量坍缩结果的随机性。量子随机性来源于量子叠加态的波函数坍缩，与任何经典理论不存在关联，也不存在于任何经典理论框架中。需要注意的是，虽然量子随机性是量子理论中独有的特性，但并不代表某个QRNG的随机源能够被量子理论所描述，这个QRNG就具有良好的量子随机性，也并不是只要系统处于量子纯态，测量结果就能够展现量子随机性。其一，在理论框架上，量子随机性仅属于量子力学理论的一部分，即量子测量坍缩假设的部分。而量子理论中的其余部分不产生内禀随机性，例如量子系统的幺正演化虽然遵循薛定谔方程，但其仍是确定性的方程，在期望值上和经典理论相互对应，仅存在表观随机性。其二，在实际测量中，量子随机性仅来源于纯态波函数单次坍缩的力学量结果，而经典探测器的响应往往对应了大量独立纯态波函数坍缩结果的平均值，导致测量趋向于经典测量，信号趋同于经典信号，量子随机性趋于零。在QRNG应用中，即使随机源是一个纯态量子源，若测量结果是大量纯态测量坍缩结果的平均值，其信号的量子随机性也会趋于零。

以光为例，单光子级的光场测量结果能够展现出显著的量子涨落。而随着光强增强，探测器响应的独立光子数不断增加，测量结果不再是单个光子态坍缩的结果，而变为大量光子态坍缩结果的平均值，其值与经典电磁波理论所描述的一致，即量子特性消失，不表现出量子随机性。因此探测过程作为测量坍缩的一部分也对QRNG量子随机性存在显著的影响，在QRNG设计中需要被仔细考虑。例如若单光子路径选择型QRNG中将单光子探测器换成简单的光强探测器，单光子源换成脉冲光源，那么探测器的信号是大量光子态坍缩的平均光子数，该QRNG的随机性为表观随机性。

与经典随机信号相比，量子随机性的最大特性是独立同分布(independent and identically distributed，IID)特性。

5.2　独立性

独立性是量子叠加态坍缩的本质属性。叠加态的波函数坍缩是瞬时过程，信号上表现为阶跃过程，坍缩结果与系统的历史状态无关，天然具有独立性，例如对于电子自旋叠加态|ψ>=|↑>+|↓>，即使两次测量坍缩的量子态完全相同，测量条件也完全相同，两次坍缩的结果也是独立的，各自独立等概率地出现↑或↓的测量结果。而与波函数坍缩过程相反，经典系统局域时间信号必然存在相关性。其一，从源的角度看，经典物理系统按确定性的正则方程演化，带宽有限，相关性不可避免，例如电路中的经典电磁噪声，由于电路中不可避免的分布电容、分布电感效应，电信号不存在信号的阶跃突变，局域时间内的信号必然存在显著关联，根据奈奎斯特采样定理[26]，只要采样信号大于系统信号带宽的两倍，就能够恢复原有信号。其二，从探测器的角度看，经典信号对应于探测器响应时间范围内大量粒子物理量的平均值，探测器输出信号响应时间范围内的相关性也不可避免。以光功率计为例，其带宽有限，测量结果是一段时间内光功率的平均值，输出的光功率结果不存在突变，即局域时间内的信号必然存在关联。综上，独立性是量子随机性与经典随机性的本质区别。

5.3　同分布性

同分布性是量子叠加态等概率坍缩的必然要求，是量子随机性的必要条件。其一，在理论框架上，量子随机性是叠加态波函数坍缩产生的随机性，与量子态的幺正演化无关。量子态的幺正演化遵循薛定谔方程，在期望值上与经典理论相互对应，只存在表观随机性。只有每次坍缩前的系统被复位至相同的量子叠加态，才能保证该量子系统的坍缩结果具有相同的内禀概率分布，即理想的量子随机性。即使采用量子系统作为随机源，如果每次坍缩后量子系统没有被正确复位，那么该系统幺正演化的表观随机性将会作为噪声进入测量结果中，导致信号的量子随机性下降。例如，假设一个量子源的量子态存在幺正演化，以拉比振荡的形式为例 |ψ>=cos(Ωt/2)|0>-i sin(Ωt/2)|1>，每次测量坍缩结果的概率分布为P0(t )=cos2(Ωt/2)，P1(t)=sin2(Ωt/2)，这类演化(正弦函数)显然是确定性的演化，但若QRNG系统对此不加区分，将其也作为随机输出的一部分，那么这些幺正演化的部分就作为表观随机性(噪声)混入了最终输出，虽然统计结果上依然能满足，但其中表观随机的部分将与拉比频率Ω等外界条件(例如外部磁场)产生关联，导致量子随机性降低。其二，在实际测量中，测量系统的不变性也要求了每次测量前应当保证量子系统被正确复位。总而言之，量子随机性来源于波函数的瞬时坍缩，不存在任何演化过程，而经典表观随机性恰是来源于信息不足的随机演化，这也是量子随机性和经典随机性的本质区别。非同分布就意味着系统状态存在演化，存在演化就代表系统存在表观随机性，因此同分布性是量子随机性的必要条件之一。

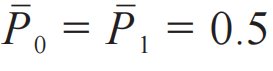
从量子随机性的定义与特性可以看到，并非只要使用了量子系统作为随机源，就能保证QRNG具有良好的量子随机性。实际QRNG系统必然包含了控制、采样等经典部分，输出的随机信号不可避免地包含量子随机性与非随机、表观随机性的成分，其中仅有纯态坍缩的量子随机性是内禀随机的。可将除去量子随机性的部分定义为QRNG系统的噪声，将QRNG系统的量子性定义为量子随机性所占比例：

噪声广泛存在于整个系统，包括量子随机源与测量、采样系统等，产生的原因也不尽相同。对于量子随机源，系统量子态由于环境扰动、状态制备不完美等因素发生的演化就是一种噪声。这类演化理论上是确定性的，具有有限带宽，能够通过反馈、补偿等方式进行抑制，而量子态坍缩信号作为量子系统本质属性并不会受这些操作的影响。对于测量与采样系统，测量设备误差与不稳定是一种噪声。由于实际测量系统为经典系统，带宽有限，与波函数瞬时坍缩无限大的等效带宽存在矛盾，即使随机源是理想的量子系统，根据塔拉格朗的结论，如果每次采样对应了多个粒子的坍缩，这些粒子的随机性倾向于相互抵消，导致信号的随机性下降，这也是系统的噪声。此外如果采样系统带宽大于信号带宽，根据奈奎斯特采样定律，采样结果本身将具有相关性，导致量子性损失，这也是一种噪声。

对于QRNG系统而言，仅有量子随机性的部分是我们所需的信号，其余的部分均为噪声。但由于噪声也具备一定“无序”(统计上无序但非内禀随机)的特点，部分QRNG工作中忽视了对于量子随机性与噪声的分析，简单地将噪声也视为系统随机性的一部分，导致随机信号中量子随机性的比例较低，系统量子性不显著。这样的QRNG系统和经典随机系统相比不存在量子优势，也就失去了其在安全性上本应具备的重要意义。因此QRNG的量子性在设计与检测中是一个被忽视但却十分重要的问题。

06量子时代密码系统发展现状

量子计算技术正在迅速发展，并且发展速度大大超过了许多人的预期，量子计算对现有密码体系的威胁进度远比想象中要快，这也成为了传统密码体系头顶的达摩克里斯之剑。为了对抗量子计算对现有密码体系的破坏，2024年8月13日，美国NIST正式发布首批后量子加密(post-quantum cryptography，PQC)标准，旨在利用更复杂的算法以抵御量子计算机的威胁。但由于目前对于量子计算算法的研究尚不充分，PQC算法只能抵御已知的量子密码破解算法，量子计算机的能力上限也尚不明确，因此对于PQC算法能否完全抵御量子计算攻击仍存在争议。利用PQC来应对量子计算机的方式只是一种过渡方案，密码体系正向着超越计算复杂性、依赖量子物理原理与随机数的不可预测性来保证安全的方向发展。未来随机数将完全成为密码体系安全性的保障，QRNG也将成为密码体系的核心。

目前已经有很多QRNG技术方案被提出，并且很多方案都已实现可实用化与芯片化，主要可以分为两类：一类是基于光子体系的QRNG，包括光子路径选择、光子到达时间、光子相位涨落与光的真空涨落等技术方案[16，27—33]；另一类是基于电子体系的QRNG，包括雪崩二极管、隧道二极管与范德瓦耳斯异质结等技术方案[34—36]。

6.1　基于光子体系的量子随机数发生器

量子光学的实验技术比较成熟，包括高性能量子光源、单光子探测技术、光纤技术以及各种灵活的光学元件等。目前实验室对于光子的操控普遍具有较高水平，因此光子系统在性能与工程实现难度上达到了良好的平衡，成为当前QRNG的主流实现方案。但由于光子测量过程涉及到了光电转换等诸多经典物理过程，降低了熵源输出的原始数据的随机性，因此光子体系的QRNG依赖对原始数据的数学后处理。不过后处理是确定性的数学过程(如Toeplitz hash算法)，不会增加原始数据的随机性。对光子体系QRNG而言，如何提升熵源原始数据的随机性仍然是一大挑战。基于相位涨落与真空涨落的方案是目前光子体系QRNG中实用化较高的方案，以下进行简单的介绍。

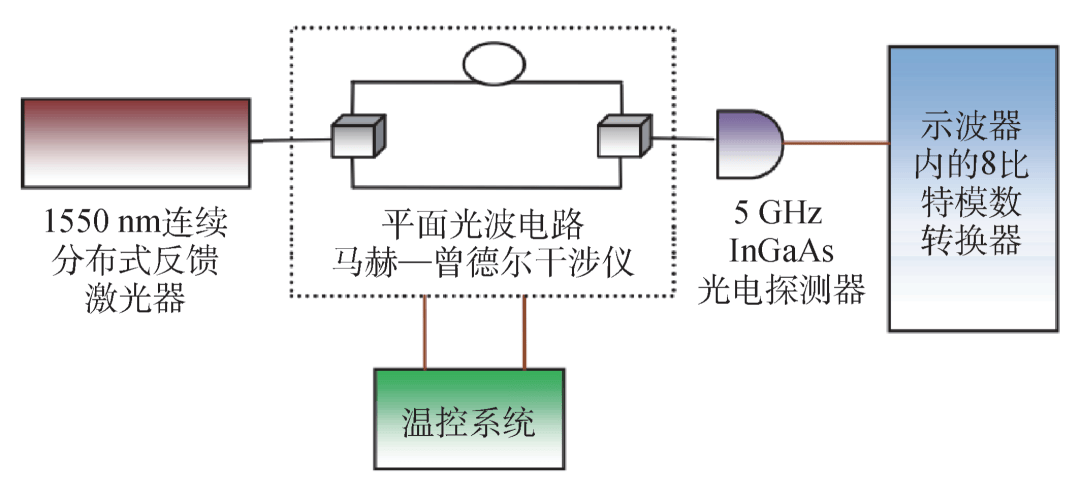图6　基于相位涨落QRNG的原理图[27]

基于相位涨落的QRNG利用激光器内自发辐射效应导致的光场相位随机量子涨落，通过干涉仪将相位涨落转换为强度涨落来输出随机数，如图6所示。2012年，清华大学研究组利用激光相位涨落实现了随机数生成，验证了量子相位涨落作为随机源的可行性[27]。2015年，中国科学技术大学研究组将相位涨落QRNG速率提高至68 Gbps[28]。目前，基于相位涨落的QRNG已实现了集成化与实用化(实时后处理输出)[29，30]，是主流QRNG方案之一。

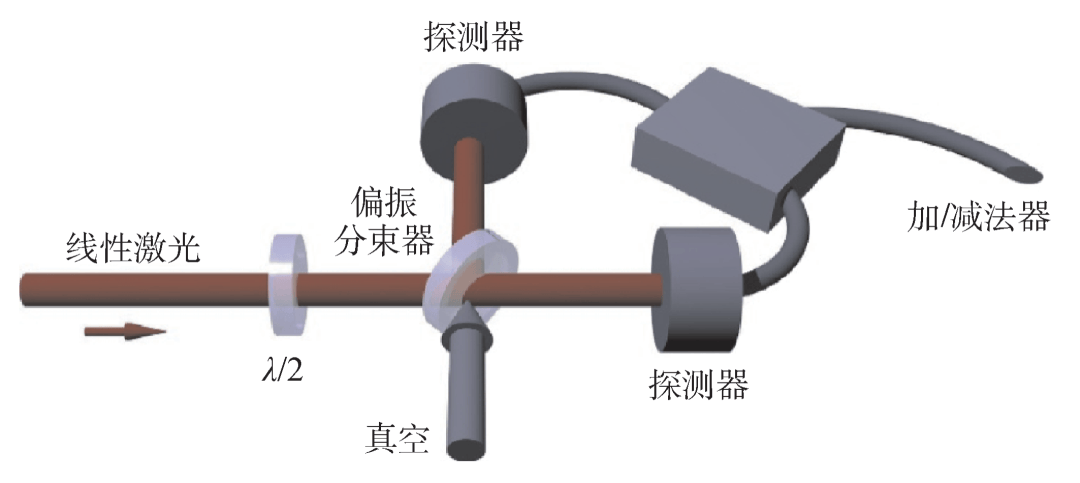图7　基于真空涨落QRNG的原理图[31]

基于真空涨落的QRNG利用不确定性原理导致的光场真空态涨落，通过平衡零差检测等技术将真空涨落转化为电信号输出随机数，如图7所示。2010年，德国马克斯普朗克研究所利用真空态正交振幅的不确定性实现了6.5 Mbps的随机数输出[31]。同年，国防科技大学研究组将真空涨落的QRNG输出速率提升至12 Mbps[32]。目前该方案的QRNG也实现了集成化与实用化[37]。

6.2　基于电子体系的量子随机数发生器

电子体系的QRNG通常基于固体内的电子隧穿效应来输出随机数。当固体中的势垒宽度较窄时，处于势阱中的电子有概率越过能量高于自身的势垒，形成隧穿电流。隧穿效应是典型的量子效应，具备内禀随机性。与光子体系相比，电子体系QRNG不存在电—光—电转换过程，能够避免转换过程中的经典噪声，未经后处理的原始序列质量普遍更高，在随机性与安全性上更具优势。

2017年，英国兰卡斯特大学研究组利用隧道二极管内的电子隧穿效应实现了随机数输出[34]。2022年，基于范德瓦耳斯异质结的QRNG被提出，在不存在任何数学处理的条件下，NISTSP800-90B认证最小熵达到了0.983 bits/bit，是当时QRNG的最高记录[35]。2023年，清华大学研究组利用雪崩二极管内的电子隧穿效应实现了100 Mbps的随机数输出，在无任何后处理的条件下，NIST SP 800-90B认证最小熵达到了0.9872 bits/bit，首次实现了实用化的电子体系QRNG。

07总 结

随机数是信息安全的基石。随着人们对于随机性的理解加深，量子力学中的内禀随机性对于信息安全的重要性越来越显著，QRNG领域也正处于百花齐放的时代。作为信息安全系统中最重要的基础设施，QRNG正向着高随机性、高稳定性、高输出率、高集成性的方向发展，将在未来的信息网络安全中发挥不可替代的作用，我们期待着这一天的到来。

致 谢 感谢清华大学物理系朱邦芬教授在本论文立意、框架等方面给予的具体指导。感谢邵舜先生和首都师范大学物理系杨哲老师在论文立意方面的启发与支持。

参考文献：

[1] Bouda J，Pivoluska M，Plesch M et al. Physical Review A，2012，86(6)：062308

[2] Li H W，Yin Z Q，Wang S et al. Scientific Reports，2015，5(1)：16200

[3] Li M，Vitányi P. An introduction to Kolmogorov complexity and its applications. New York：Springer，2008.pp.49—56

[4] Van Lambalgen M. Random Sequences. Amsterdam：University of Amsterdam，2014. pp.1—160

[5] Kolmogorov A N. Problems of Information Transmission，1965，1(1)：1

[6] Martin-Löf P. Information and Control，1966，9(6)：602

[7] Bassham L，Rukhin A，Soto J et al. A Statistical Test Suite for Random and Pseudorandom NumberGenerators for Cryptographic Applications. Gaithersburg：National Institute of Standards and Technology Special Publication，2010. pp.1—131

[8] 密码行业标准化技术委员会 . GM/T 0005-2021：随机性检测规范. 北京：中国标准出版社，2021. pp.1—32[9] Kolmogorov A N. Russian Mathematical Surveys，1983，38(4)：29

[10] Kolmogorov A N. On Logical Foundations of Probability Theory. In：Prokhorov J V， Itô K eds. Probability Theory and Mathematical Statistics. Berlin，Heidelberg：Springer Berlin Heidelberg，1983. pp.1—5

[11] Freudenthal H. Realistic Models in Probability. In：Lakatos I，eds. Studies in Logic and the Foundations of Mathematics. London：Elsevier，1968. pp.1—23

[12] Von Neumann J. Appl. Math. Ser.，1951，12(3)：36

[13] Pareschi F，Setti G，Rovatti R. IEEE Transactions on Circuits and Systems I-Regular Papers，2010，57(12)：3124

[14] Gong L S，Zhang J G，Liu H F et al. IEEE Access，2019，7：125796

[15] Von Neumann J. Mathematical Foundations of Quantum Mechanics：New edition. Princeton：Princeton University Press，2018.pp.1—303

[16] Jennewein T，Achleitner U，Weihs G et al. Review of Scientific Instruments，2000，71(4)：1675

[17] Penrose O. Reports on Progress in Physics，1979，42(12)：1937

[18] Laplace P S. Théorie analytique des probabilités. Paris：V. Courcier，1820. pp. vi—vii

[19] Bell J S. Physics Physique Fizika，1964，1(3)：195

[20] Aspect A，Dalibard J，Roger G. Phys. Rev. Lett.，1982，49(25)：1804

[21] Aspect A，Grangier P，Roger G. Phys. Rev. Lett.，1981，47(7)：460

[22] Freedman S J，Clauser J F. Phys. Rev. Lett.，1972，28(14)：938

[23] Bennett C H，Brassard G，Crépeau C et al. Phys. Rev. Lett.，1993，70(13)：1895

[24] Talagrand M. The Annals of Probability，1996，24(1)：1

[25] Ehrenfest P. Zeitschrift für Physik，1927，45(7)：455

[26] Nyquist H. Proceedings of the IEEE，2002，90(2)：280

[27] Xu F，Qi B，Ma X et al. Optics Express，2012，20(11)：12366

[28] Nie Y Q，Huang L，Liu Y et al. Review of Scientific Instruments，2015，86(6)：063105

[29] Lei W，Xie Z，Li Y et al. Quantum Information Processing，2020，19(11)：405

[30] Huang Z，Li J，Chen Y et al. Optics Express，2025，33(5)：11985

[31] Gabriel C，Wittmann C，Sych D et al. Nature Photonics，2010，4(10)：711

[32] Shen Y，Tian L，Zou H. Phys. Rev. A，2010，81(6)：063814

[33] 廖静，梁创，魏亚军 等.物理学报，2001，50(3)：467

[34] Bernardo-Gavito R，Bagci I E，Roberts J et al. Scientific Reports，2017，7(1)：17879

[35] Abraham N，Watanabe K，Taniguchi T et al. ACS Nano，2022，16(4)：5898

[36] Liu Y X，Huang K X， Bai Y M et al. Chinese Physics Letters，2023，40(7)：070303

[37] Qiao G R，Bai B，Weng Z X et al. IEEE Journal of Selected Topics in Quantum Electronics，2025，31(5：Quantum Materials and Quantum Devices)：1

来源：转载自“中国物理学会期刊网”公众号