400-004-0551
- 网站首页
- 解决方案
- 科研实力
-
产品中心
- 量子安全智能办公硬件
- 量子安全高拍仪
- 量子安全笔记本电脑
- 量子安全云智能Pad
- 量子安全云办公一体机
- 量子安全云智能签字笔
- 量子安全手表
- 量子安全智能鼠标
- 量子安全智能工牌
- 量子安全水滴
- 量子安全智能办公软件
- 量子安全办公OA软件
- 量子安全智能印签系统
- 客户&伙伴
- 合作生态
- 视频中心
- 新闻中心
- 关于云玺

news center
新闻中心
发布时间:2023-03-03 10:34:12 信息来源: 阅读次数: 7276 次
导读:
在科幻电影中,经常有把人从一个地方瞬间传送到另一个地方的镜头。《星际迷航》最经典的台词就是:“把我传上去(Beam me up)!”这种传送术并不是完全的幻想,它的科学原理就是量子隐形传态。现在离传送人还很远,但已经能传送一个光子了,——这已经很不容易啦!
—————————————————————————————————————————
前文参见:
十一、量子搜索
设想有一部杂乱无章的N个人名的花名册,其中的人名没有按照任何特别的顺序排列,而且每个名字可能出现不止一次。你想在其中找到某个名字,如“张三丰”,该怎么办呢?(张三丰:为什么要找老道?回答:谁叫你把花名册弄得杂乱无章的!)
在经典框架下,最好的算法也就是最老实的算法:从头看到尾。如果运气好,第一个就是张三丰;如果运气不好,到最后一个即第N个才找到张三丰。平均而言,这需要N/2次操作。如果N表示成二进制有n位,那么计算量就是2n-1的量级,又是指数增长,不可计算。这个结果不可能改进了,因为排列顺序是完全没有规律的。
但是量子计算机却能够改进。1996年,格罗弗(Lov K. Grover)提出了一种搜索的量子算法。基本思路是:把所有的解(搜索问题的解可能不止一个)对应的态矢量记为|ω>,初始状态对应的态矢量记为|s>。我们不知道|ω>是什么,但格罗弗的算法可以把态矢量向|ω>的方向旋转,每次旋转都靠近一点。经过N的平方根量级的步数,就可以以50%的置信度找到解。
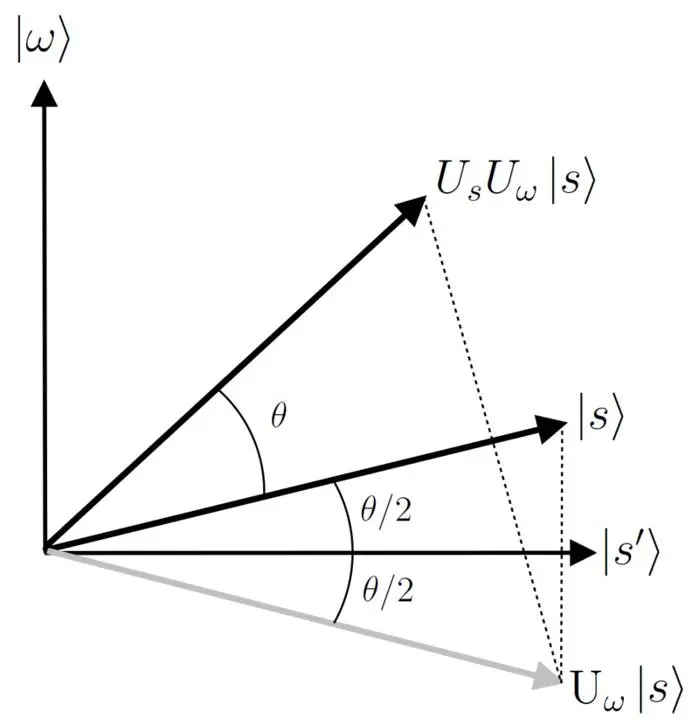
量子搜索。|ω>是搜索问题所有解的叠加,|s′>垂直于|ω>,初始状态|s>与| s′>的夹角为θ/2,每次迭代都把态矢量向|ω>的方向旋转θ角度
把整个过程每重复一次,都会把不确定度减半。如果迭代10次,不确定度就会下降到1/210 = 1/1024,大约是0.1%,也就是说置信度上升到99.9%。所以只要你先定个置信度的“小目标”,比如说99%或99.99%,只要不是100%就行,量子搜索算法很快就会给你达到,计算量没有定性的提高,仍然是√N的级别。
量子搜索算法付出的代价,是结果不再是完全确定的。有可能你本来想找张三丰,实际找到的却是张无忌。(张无忌:怪我咯?)但好处是计算量从N的级别下降到了√N的级别,而不确定程度可以随需求任意减少,大不了多迭代几次。(张三丰,这次你跑不了了!)
经典搜索算法不能改进,是因为它只能给出确定的答案,找到了就是找到了,没找到就是没找到。但只要你放弃这个刚性的要求,接受以一定的概率找到解(这个概率可以非常接近100%),量子搜索算法就可以减少计算量。这实际上是各种问题的量子算法的一个普遍特点。
因数分解的量子算法对经典算法是指数级的改进,把不可计算变成了可计算。无格式搜索的量子算法对经典算法却只是平方级的改进,√N = 2n/2还是指数增长,没有发生质的变化,仍然是不可计算。但是这个改进已经非常大了。如果N等于一亿,这就是一万倍的节约。
一类问题不可计算的意思,并不是完全不能计算,而是在问题的尺度大到一定程度后算不动。量子搜索带来的计算量下降,可以使算不动的界限大大地向外推,使在实际条件下能够计算的问题范围大大增加。由于搜索是非常常见而重要的问题,所以量子搜索的重要性并不逊于量子因数分解,甚或犹有过之。
十二、量子隐形传态
前面介绍了两个量子计算的例子,下面我们来看量子通信的例子。
在科幻电影中,经常有把人从一个地方瞬间传送到另一个地方的镜头。《星际迷航》最经典的台词就是:“把我传上去(Beam me up)!”这种传送术并不是完全的幻想,它的科学原理就是量子隐形传态。现在离传送人还很远,但已经能传送一个光子了,——这已经很不容易啦!

《星际迷航》中的传送术
量子隐形传态到底是什么呢?它是1993年设计出来的一种实验方案,把粒子A的量子状态传输给远处的粒子B,让粒子B的状态变成粒子A最初的状态。请注意,传的是状态而不是粒子,两个粒子的空间位置都没有变化。好比A处有一辆汽车或一个人,不是把这辆汽车或这个人搬到B处,而是把B处本来就有的一堆汽车零件或原子组装成这辆汽车或这个人。
有人要问了:那岂不是得到了相同的两个人?!哪个是真正的自己?!在你为伦理问题浮想联翩、诗兴大发前,一句话就可以消灭这个问题:不会出现相同的两个人。大自然早有安排,掐断了这种可能性。(好讨厌,人家真的想做诗了啦!)
在量子隐形传态中,当B粒子获得A粒子最初的状态时,A粒子的状态必然改变。在任何时刻都只能有一个粒子处于目标状态,所以只是状态的“移动”,而不是“复制”。一定要说复制的话,也是一种破坏性的复制。好比武侠小说中前辈把功力传给主角,传完后前辈就没有功力了,而不是出现两个高手(《天龙八部》中的无崖子和虚竹频频点头)。敢情武林高手们都自带量子隐形传态功能,——无线快充,你值得拥有!

无崖子把功力传给虚竹
很多人听说量子力学中状态的变化是瞬时的,无论两个粒子相距多远,于是认为量子隐形传态可以biu的一声把人传到任意远的地方,超过光速,推翻相对论。超光速传输!破碎虚空!亦可赛艇!很遗憾,这个理解又是错误的。(吃瓜群众的心碎了……)
在做测量的时候,如前面所说,状态的变化确实是瞬时的,不需要花费时间。但是量子隐形传态的方案包括若干步,其中一步是把一个两比特的信息(即00、01、10、11这四个字符串之一)从A处传到B处,B根据这个信息确定下一步做什么(在四种待选的操作中选择一个),才能把B粒子的状态变成目标状态。这个信息需要用经典的通信方式(例如打电话、发邮件)传送,速度不能超过光速,所以整个量子隐形传态的速度也不能超过光速。
用一个比喻来说,你开着一辆超级跑车狂奔,但遇到一段堵车的路,那么你在其他路段跑得再快也没用,整个行程的速度都被这段堵车拖下来了。虽然把光速称为一个拖后腿的“慢速”显得有点滑稽(光子:我真的跑得很慢吗?有种你出来跟我比比!),但道理就是这个道理。
其实,所有的量子信息实验方案都是基于已知的物理原理设计出来的,每一个步骤都在量子力学和相对论的预言范围之内,所以怎么可能违反已知的原理呢?你应该把量子信息理解成一种在现有理论框架下的充满创造力的工程成就,好比长城、赵州桥、高铁、宇宙飞船,而不是一种颠覆现有理论框架的科学革命。
还有一个很容易产生的误解,是以为量子隐形传态是先扫描出A处的物或人的状态,再在B处组装一个相同的物或人。非也非也,量子隐形传态不是CT扫描。如果要先知道目标状态,那还有什么意思?量子隐形传态是在不知道A粒子状态的情况下,把B粒子变成这个状态!就像送快递,不知道送的是什么东西,但保证原原本本地送到。(东风快递,使命必达,欧耶。)

东风快递
而且你千万不要试图去知道A粒子的状态哦!一旦你做测量,就强迫A粒子的状态落到了基组中的一个状态上面,整个量子隐形传态都鸡飞蛋打了,而你还是不知道A原来是什么状态。(听着好像《三国演义》中魏延踢翻七星灯,破坏了诸葛亮禳星延寿的故事?姜维拔剑砍魏延:早就跟你说要好好学量子力学了!)

诸葛亮禳星
这里涉及到一个有趣的要点。在宏观世界里复制一本未知的书或一个未知的电脑文件是很容易的,在量子力学中却不能复制一个粒子的未知状态(关键是“未知”,如果你知道这个状态是什么,当然可以制备许多跟它一样的)。也就是说,未知的经典比特可以复制,未知的量子比特却不能复制。这是量子与经典的一个本质区别,叫做“量子态不可克隆定理”。
因此,在经典计算机中有复制这个操作(我们整天用),在量子计算机中却没有复制操作(想想看,这是多么奇怪的计算机啊!)。在这个定理的限制下,量子隐形传态做到的,已经是对一个未知的量子态能做的最精妙的操作了:移动,而不是复制。所以在未来的量子计算机中,量子隐形传态是一个基本的元素,人们希望用它来传输量子比特。
总而言之,量子隐形传态是以不高于光速的速度、破坏性地把一个体系的未知状态传输给另一个体系。打个比方,用颜色表示状态,A粒子最初是红色的,通过量子隐形传态,我们让远处的B粒子变成红色,而A粒子同时变成了绿色。但是我们完全不需要知道A最初是什么颜色,无论A是什么颜色,这套方法都可以保证B变成A最初的颜色,同时A的颜色改变。

量子隐形传态
第一次实现量子隐形传态是在1997年,当时潘建伟在奥地利因斯布鲁克大学的塞林格(Anton Zeilinger)教授门下读博士,他们在国际顶级科学杂志《自然》上发表了一篇题为《实验量子隐形传态》(“Experimental quantum teleportation”)的文章,潘建伟是第二作者。这篇文章后来入选了《自然》杂志的“百年物理学21篇经典论文”,跟它并列的论文包括伦琴发现X射线、爱因斯坦建立相对论、沃森和克里克发现DNA双螺旋结构等等。
18年后的2015年,这时潘建伟是中国科学技术大学教授、中国科学院院士,他和陆朝阳等人在《自然》上发表了《单个光子的多个自由度的量子隐形传态》(“Quantum teleportation of multiple degrees of freedom of a single photon”),新的成果是“多个自由度”。这项成果被英国物理学会评为2015年十大物理学突破之首。

媒体报道我国首次实现多自由度量子隐形传态
艾数学同学,你问自由度是什么?自由度就是描述一个体系所需的变量的数目。例如一个静止在一条线上的粒子,描述它只需要一个数,自由度就是1。静止在一个面上的粒子,自由度就是2。静止在三维空间中的粒子,自由度就是3。描述三维空间中一个运动的粒子,需要知道位置的3个分量和速度的3个分量,自由度就是6。
光子具有“自旋角动量”和“轨道角动量”,如果你看不懂这两个词,没关系,只要明白它们是两个自由度就够了。在1997年的实验中,传的只是自旋。此后各种体系的各种自由度都被传输过,但每次实验都只能传输一个自由度。
传输一个自由度已经很不容易了,但是这只具有演示价值。量子隐形传态真的要实用,要传物传人,就必须传输多个自由度。这在理论上是完全可以实现的。打个比方,现在用颜色和形状来表示状态,A粒子最初是红色的正方形,我们可以让B粒子变成红色的正方形,同时A变成绿色的圆形。
这个扩展看似显而易见,但跟传输一个自由度相比,实验难度提高了非常多。量子隐形传态需要一个传输的“量子通道”,这个通道是由多个粒子组成的,这些粒子纠缠在一起,使得一个粒子状态的改变立刻造成其他粒子状态的改变。(赶快回顾一下纠缠态的定义!)
让多个粒子在一个自由度上纠缠起来,已经是一个很困难的任务了,而要传输多个自由度,就需要制备多粒子的多个自由度的“超纠缠态”,更加令人望而生畏。潘建伟研究组就是攻破了这个难关,搭建了6光子11量子比特的自旋-轨道角动量纠缠实验平台,才在2015年实现了自旋和轨道自由度的同时传输。

潘建伟在调试设备(资料图片)新华社记者 张端/摄
《道德经》说:“道生一,一生二,二生三,三生万物。”我们可以说量子隐形传态1997年实现了道生一,那时潘建伟还是博士生。2015年实现了一生二,这时他已经是量子信息研究的国际领导者。从传输一个自由度到传输两个自由度,走了18年之久。这中间有无数的奇思妙想、艰苦奋斗,是人类智慧与精神的伟大赞歌。
好,我们现在终于可以传送一个光子的两个自由度了,那么离电影里的传送人还有多远的距离呢?来估算一下。
12克碳原子是1摩尔,即6.023 × 1023个。人的体重如果是60公斤,就大约有5000摩尔的原子,3 × 1027个。描述一个原子的状态,要多少个自由度?姑且算作10个吧。那么要描述一个人,就需要1028量级的自由度。我们刚刚从1进步到了2……所以,嗯,我们的征途是星辰大海!向着夕阳奔跑吧,少年!

向着夕阳奔跑吧,少年!
(未完待续)
背景简介:本文作者为袁岚峰,中国科学技术大学化学博士,中国科学技术大学合肥微尺度物质科学国家实验室副研究员,科技与战略风云学会会长。