你完全可以理解量子信息（14）| 袁岚峰

导读：

不少科普作品说量子密码术离不开量子纠缠，这就大错特错了！实际上，量子密码术有若干种实现方案，有些用到量子纠缠，有些不用量子纠缠。对于实验来说，操纵多个粒子肯定比操纵一个粒子困难。所以，用单粒子方案，也就是说不用量子纠缠，才能达到最优的效果。

前文参见：

你完全可以理解量子信息（1） | 袁岚峰

你完全可以理解量子信息（2-3） | 袁岚峰

你完全可以理解量子信息（4-5） | 袁岚峰）

你完全可以理解量子信息（6） | 袁岚峰）

你完全可以理解量子信息（7） | 袁岚峰

你完全可以理解量子信息（8-10）| 袁岚峰

你完全可以理解量子信息（11-12）| 袁岚峰

你完全可以理解量子信息（13）| 袁岚峰

十四、量子密码术的实现方法

什么样的操作，能在通信双方产生一段相同的随机数序列呢？

如果你是一个真正聪明而细心的读者，你就会想起本文前面关于EPR实验的一句话（http://weibo.com/ttarticle/p/show?id=2309404152264544625278）：“A测量粒子1得到的是一个随机数，B测量粒子2得到的也是一个随机数，只不过这两个随机数必然相等而已。”

妙啊！那一段是解释为什么EPR实验不能传输信息，但有了量子密码术的背景知识，你就会领悟到，把这个过程重复多次，双方得到的相同的随机数序列就可以用作密钥。然后你可以用这个密钥传输信息。这和“EPR实验不传输信息”并不矛盾，因为传输信息时用的是普通的通信方式，不是EPR实验。

很好，利用量子纠缠，我们立刻就找到了一种量子密码术的方案。这至少说明量子密码术是可以实现的，证明了它的存在性。

量子密码术

但是，不少科普作品说量子密码术离不开量子纠缠，这就大错特错了！这种说法造成了很多困扰。实际上，量子密码术有若干种实现方案，有些用到量子纠缠，有些不用量子纠缠。量子纠缠是个可选项，而不是必要条件。

不仅如此，稍微想想你还会明白，量子纠缠是一种多粒子体系的现象，而对于实验来说，操纵多个粒子肯定比操纵一个粒子困难。所以，只要有单粒子的方案，人们必然会优先用单粒子方案。实际情况正是如此，绝大多数量子密码术的实验都是用单粒子方案做的，这样才能达到最优的效果。而基于量子纠缠的量子密码术方案，就像用火箭送快递一样不实用，只具有理论意义。

当然，这不是说量子纠缠没用。对于整个量子信息学科来说，量子纠缠非常有用，例如量子隐形传态就以量子纠缠为基础，但那是量子密码术之外的应用了。正是因为量子密码术可以不用量子纠缠，所以它的技术难度在量子信息的各种应用中是最低的（只是相对而言，绝对的难度还是很高），所以它发展得最快，最先接近了产业化。

不用量子纠缠，怎么在双方产生相同的随机数序列？想想前面介绍的“三大奥义”，真正产生随机数的是对叠加态的测量。所以只要充分利用叠加和测量这两个手段，单个粒子就可以在双方产生相同的随机数。在“三大奥义”中，量子密码术只需要前两个（叠加、测量）就够了，不需要第三个（纠缠）。

科学家们把量子密码术的方案都称为某某协议（就像计算机科学中的“TCP/IP协议”），上述利用EPR对的方案叫做EPR协议，而单粒子的方案包括BB84协议、B92协议、诱骗态协议等等。BB84协议是美国科学家Charles H. Bennett和加拿大科学家Gilles Brassard在1984年提出的，BB84是两人姓的首字母以及年份的缩写。BB84协议是最早的一个方案，而且目前最先进的诱骗态协议可以理解为它的推广。所以只要理解了BB84协议，就理解了量子密码术的精髓。

在BB84协议中，用到光子的四个状态：|0>、|1>、|+>和|->。Hi，四位老朋友，又见面了~（|0>、|1>、|+>和|->：我们叫做“江南四大才子”！）在实验上，这四个状态是用光子的偏振（回顾一下，偏振方向就是电场所在的方向）来表示的，分别对应光子的偏振处于0度、90度、45度和135度。

江南四大才子

让我们回忆一下，|0>和|1>这两个态构成一个基组，|+>和|->这两个态构成另一个基组。在某个基组下测量这个基组中的状态，比如说在|0>和|1>的基组中测量|0>，那么结果不变，测完以后还是|0>这个态。在某个基组下测量这个基组之外的状态，比如说在|0>和|1>的基组中测量|+>，那么结果必然改变，以一半的概率变成|0>，一半的概率变成|1>。

好，现在我们来叙述BB84协议的操作过程。A拿一个随机数发生器（通俗地说就是掷硬币），产生一个随机数0或者1（让我们把它记作a），根据这个随机数决定选择哪个基组：得到0就用|0>和|1>的基组，得到1就用|+>和|->的基组。选定基组之后，再产生一个随机数（记作a′），根据这第二个随机数决定在基组中选择哪个状态：得到0就在|0>和|1>中选择|0>或者在|+>和|->中选择|+>，得到1就在|0>和|1>中选择|1>或者在|+>和|->中选择|->。经过这样双重的随机选择之后，A把选定状态的光子发送出去。

B收到光子的时候，并不知道它属于哪个基组。他怎么办呢？他可以猜测。B也拿一个随机数发生器，产生一个随机数（记作b），得到0的时候就在|0>和|1>的基组中测量，得到1的时候就在|+>和|->的基组中测量。B测得|0>或者|+>就记下一个0，测得|1>或者|->就记下一个1，我们把这个数记为b′。

看出来了吧？如果B猜对了基组，a = b，那么光子的状态就是B的基组中的一个，所以测量以后不会变，a′必然等于b′。而如果B猜错了基组，a ≠ b，那么光子的状态就不是B的基组中的一个，所以测量后会突变，a′和b′就不一定相等了（有一半的概率不同）。

把这样的操作重复若干次，双方发送和测量若干个光子。结束后，双方公布自己的a和b随机数序列（“公布”的意思就是对全世界公开，就是这么任性~），比如说a的序列是0110，b的序列是1100。然后找出其中相同的部分，在这个例子里就是第二位（1）和第四位（0）。

现在我们知道了，在第二位和第四位，a′和b′必然是相同的！A和B把各自手里第二位和第四位的a′和b′记下来，这个随机数序列就可以用作密钥。如果发送和接收n个光子，由于B猜对基组的概率是一半，就会产生一个长度约为n/2位的密钥。至于a、b两个序列中不同的部分，在这个例子中就是第一位（0对1）和第三位（1对0），它们对应的a′和b′有可能不同，所以我们就不去看它们了，这部分数据直接抛弃。

不过，到目前为止我们都假定只有A、B双方在通信，没有敌对方在窃听。作为一个保密的方法，需要回答的下一个问题是：在有人窃听的情况下，如何保证密钥不被偷走？

让我们把这个窃听者称为E（联想英文单词evil，“邪恶的”）。料敌从宽，我们还假设E非常神通广大，A发给B的每一个光子都先落到了他手里。BB84协议有一个办法，使得即使在这种最不利的情况下，E也偷不走情报。

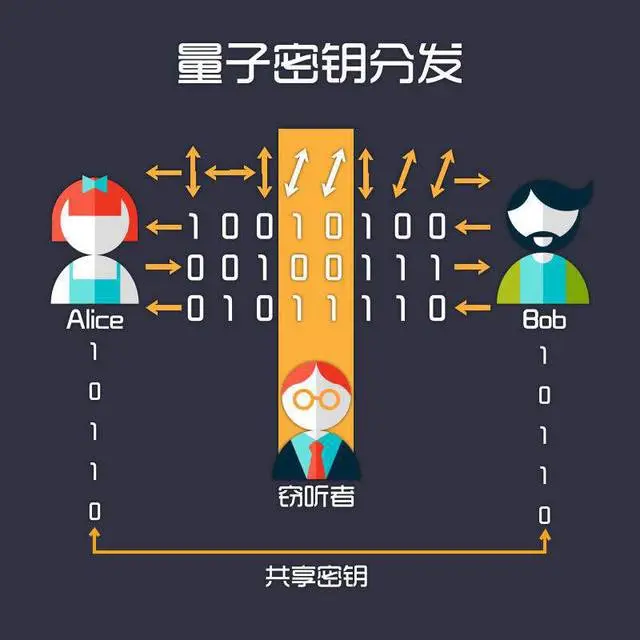
量子密钥分发

什么办法呢？站在E的角度上想一想。如果E只是把这个光子拿走，那么他只是阻断了A、B之间的通信，仍然拿不到任何信息。E希望的是，自己知道这个光子的状态，然后把这个光子放过去，让B去接收。这样A和B看不出任何异样，不知道E在窃听，而在A和B公布a和b序列后，E看自己手上的光子状态序列，也就知道了他们的密钥。

但是E的困难在于，他要知道当前这个光子处在什么状态，就要做测量。可是他不知道该用哪个基组测量，那么他只能猜测。这就有一半的概率猜错，猜错以后就会改变光子的状态。

例如A发出的状态是|+>（这对应于a= 1, a′ = 0），E用|0>和|1>的基组来测量|+>，就会以一半的概率把它变成|0>，一半的概率把它变成|1>，然后B再去测量这个光子。如果B用的基组是|0>和|1>（b = 0），公布后会发现这里a ≠ b，这个数据就被抛弃。而如果B用的基组是|+>和|->（b = 1），公布后会发现这里a = b, 这个数据要保留。这时b′等于什么呢？无论是|0>还是|1>，在|+>和|->的基组下测量时都以一半的概率变成|+>（b′ = 0），一半的概率变成|->（b′ = 1）。因此，a′和b′有一半的概率出现不同。

稍微想一下，你就会发现这是普遍的结果：只要E猜错了基组，a′和b′就会有一半的概率不同。E猜错基组的概率是一半，所以总而言之，在E做了测量的情况下a′和b′不同的概率是1/2 × 1/2= 1/4。这就是窃听行为的蛛丝马迹。

那么，通信方的应对策略就呼之欲出了。为了知道有没有窃听，A和B在得到a′和b′序列后，再挑选一段公布。这是BB84协议中的第二次公布。你看，有时为了保密，我们必须要“公布”，而且“公布”会成为一个威力巨大的保密武器。假如在公布的序列中出现了不同，那么他们就知道有人在窃听，这次通信作废。

这样做的效率怎么样呢？公布一个字符，E蒙混过关的几率是3/4。公布两个字符，就是3/4的平方。如果公布m个字符，E蒙混过关的概率就是3/4的m次方。这个概率随着m的增加迅速接近于0，例如当m = 100时，只剩下3.2× 10-13。因此，如果公布了很长一段都完全相同，那么就可以以接近100%的置信度确认没有窃听，通信双方就把a′和b′序列中剩下的部分作为密钥。

如果发现有窃听，那么该怎么办？如果有多条信道的话，你可以换一条信道，除非敌人把所有的信道都卡死了。此外，量子密码术跟一些光学技术联用，可以确定窃听者的位置，所以你可以通知警察、国安、军队，把窃听者抓起来。这是量子密码术特有的一个巨大优势，传统密码术首先就发现不了窃听，更不用说定位了。不过这是安全部门的任务，不属于密码术的范围。至于密码术本身，在发现窃听时唯一能做的就是停止通信。因此，量子密码术规定在发现窃听时停止通信，就像谍战片里通信员被发现时第一件事就是把密码本销毁。这样就不会生成密钥，也不会发送密文，自然也就不会泄密。因此，即使在最不利的情况下，量子密码术也可以保证不泄密。

媒体经常用“绝对安全”或“无条件安全”或诸如此类的说法，来形容量子密码术。以前这些词看着一头雾水，现在你可以理解，量子密码术的安全性表现在五个方面：一，密文即使被截获了也不会被破译；二，不会被计算技术的进步破解；三，没有传递密钥的信使；四，可以在每次使用前现场产生密钥，平时不需要保存密钥；五，在密钥生成过程中如果有人窃听，会被通信方发现。这几点是量子密码术的本质特点，任何协议都是如此。

在这五个方面，传统密码术做得怎么样呢？从前面的介绍可以看出，传统密码术或者只能满足第一点、第三点和第四点（非对称密码体制，第一点依赖于数学复杂性，不是严格满足的），或者只能满足第一点和第二点（对称密码体制），无论如何都无法满足第五点。量子密码术是目前所知唯一的既不需要信使、也不惧怕算法进步的保密方法，更是唯一的能发现窃听的保密方法。一对比，就知道量子密码术的优势有多大了！

量子密码术的安全性是物理原理的产物，建立在量子力学的基础上。在有些人看来，量子力学似乎不是一个非常可靠的基础。这种心理可以理解，因为就像“三大奥义”显示的，量子力学跟日常生活经验反差巨大，不是一个很容易接受的理论。但如果你想为了破解量子密码术而推翻量子力学，那就掉到一个巨坑里去了。如前所述，量子力学经过了上百年的考验，其应用遍及现代生活的所有角落。如果你怀疑量子力学的原理，那么你是不是应该先担心自己的电脑不能工作、自己的手机打不出去呢？

对于军事和金融这样急需保密的领域，量子密码术显然具有非常高的战略意义。如果说可以破解公钥密码体系的量子计算机是最强的矛，那么能够抵御一切攻击的量子密码术就是最强的盾。以子之矛攻子之盾，谁胜？盾胜！

（未完待续）

背景简介：本文作者为袁岚峰，中国科学技术大学化学博士，中国科学技术大学合肥微尺度物质科学国家实验室副研究员，科技与战略风云学会会长